Algoritmii criptografici asimetrici au apărut ca o alternativă la algoritmii simetrici. Criptografia cu chei publice (asimetrice) a apărut în 1976 ca o soluție în gestionarea secretă a cheilor. Întregul scop al criptării este de a păstra secretul unui mesaj. În cazul criptografiei simetrice, procesul a presupus că, odată cu mesajul codificat, destinatarul ar trebui să dețină sau să primească cheia de decodare.

Criptografia asimetrică este, de asemenea, cunoscută sub numele de criptografie cu cheie publică. Aceasta înseamnă că diferite taste sunt folosite pentru procesele de codificare și decodare. În acest sistem, fiecare corespondent deține o pereche de chei: un secret și o cheie publică.

Criptografia publică folosește, în general, chei mari de criptare pentru a asigura puterea algoritmului. Compararea lungimii cheilor de criptare între diferiți algoritmi nu este întotdeauna importantă și productivă în același timp. Chiar dacă algoritmii publici consumă mai mult timp în operațiunea de codificare decât unele metode simetrice, utilizarea lor în locul celor simetrice este justificată.

Sistemele criptografice cu chei publice sunt de tip asimetric. Acestea au fost dezvoltate în special în ultimii ani, începând cu lucrările de referință ale lui Diffie și Hellman [3,5].

Algoritmul Rivest Shamir Adleman (RSA)

Criptarea RSA este un criptosistem cu cheie publică utilizat atât pentru criptare, cât și pentru autentificare, inventat de Rivest, Shamir și Adleman în 1977 [6,7].

Sistemul RSA este de tip exponențial. În această metodă, modulul n este obținut prin produsul altor două numere prime mari: n = p * q, astfel încât indicatorul lui Euler

F (n) = (p-1) * (q-1). Acesta din urmă devine mult mai dificil de determinat, iar schema poate fi utilizată cu succes într-un criptosistem cu cheie publică.

În această metodă, cheile publice e și n vor fi făcute publice, iar cheia d va fi păstrată secretă. În ceea ce privește metoda, se recomandă alegerea unui număr prim relativ d, cu F (n) în intervalul [max (p, q) +1, n-1].

În acest caz, se va calcula după cum urmează:

e = inv (d, F (n)), putând folosi o versiune extinsă a algoritmului lui Euclid.

Deoarece criptarea și decriptarea sunt reciproc inverse, metoda RSA poate fi utilizată atât pentru criptare, cât și pentru autentificare. Fiecare utilizator deține modulul și exponenții e și d. Apoi va înregistra într-un fișier cheia publică (formată din n și e), în timp ce va păstra secretul cheii d.

Un utilizator B va emite un mesaj secret M folosind transformarea publică a lui A, după cum urmează:

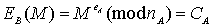
 La recepție A va primi clar mesajul, după cum urmează:

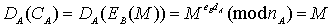
În cazul autentificării, mecanismul este următorul:

Utilizatorul A va putea semna un mesaj de la M la B prin calcularea:

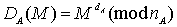
Și B va autentifica acest mesaj, folosind cheia publică a lui A, după cum urmează:

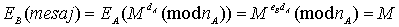
În acest fel, utilizatorul B va ști că acel mesaj vine de la utilizatorul A.

O dificultate în utilizarea criptosistemelor RSA apare atunci când sunt necesare atât protecție, cât și autentificare, deoarece sunt necesare transformări succesive cu module diferite.

De exemplu, pentru ca A să trimită lui B un mesaj semnat și criptat, A va calcula:

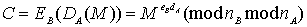
Dacă n_A>n_B blocul  D_A(M) Ï[0,n_B-1] corespunzător E_B.

Reducerea modului D_A(M)mod n_B nu rezolvă problema, neputând primi mesajul original. Soluția este de a utiliza un prag h astfel încât fiecare utilizator să poată construi două perechi de transformări pentru semnătură și protecție în condițiile:  n_{A1 < h <} n_A2