Blocks
Blocks
Funcţii Hash
Funcții Hash
O funcție care convertește datele date într-o valoare întreagă, putem presupune că o funcție hash este. Valoarea întregului mapat este utilizată ca index în tabelul hash.
O funcție hash mapează un număr mare sau un șir la un număr întreg mic care poate fi folosit ca index în tabelul hash.
O funcție hash bună ar trebui să aibă următoarele proprietăți:
Calculabil eficient.
Ar trebui să distribuie uniform tastele (fiecare poziție a tabelului este la fel de probabilă pentru fiecare tastă)
Funcții hash simple
Următoarele funcții mapează o singură tastă întreagă (k) la o mică valoare a cupei întregi h (k). m este dimensiunea tabelului hash (numărul de găleți).
Metoda divizării (Cormen) Alegeți un prim care nu este aproape de o putere de 2. h (k) = k mod m. Funcționează prost pentru multe tipuri de modele din datele de intrare.
Varianta Knuth pe Divizia h (k) = k (k + 3) mod m. Se presupune că funcționează mult mai bine decât metoda de divizare brută.
Metoda de multiplicare (Cormen). Alegeți m pentru a fi o putere de 2. Fie A un număr real cu aspect aleatoriu. Knuth sugerează M = 0,5 * (sqrt (5) - 1). Apoi faceți următoarele:
s = k*A
x = fractional part of s
h(k) = floor(m*x)
Aceasta pare a fi metoda care îi place teoreticienilor.
Pentru a face acest lucru rapid cu aritmetica întreagă, fie w numărul de biți dintr-un cuvânt (de exemplu, 32) și să presupunem că m este 2 ^ p. Apoi calculați:
s = floor(A * 2^w)
x = k*s
h(k) = x >> (w-p) SHA / Secure Hash AlgorithmAcest standard specifică algoritmi de securizare hash, SHA-1, SHA-224, SHA-256, SHA-384, SHA512, SHA-512/224 și SHA-512/256. Toți algoritmii sunt funcții hash iterative, unidirecționale, care pot procesa un mesaj pentru a produce o reprezentare condensată numită digest digest. Acești algoritmi permit determinarea integrității unui mesaj: orice modificare a mesajului va duce, cu o probabilitate foarte mare, la un rezumat diferit al mesajului. Această proprietate este utilă în generarea și verificarea semnăturilor digitale și a codurilor de autentificare a mesajelor și în generarea de numere aleatorii sau de biți.
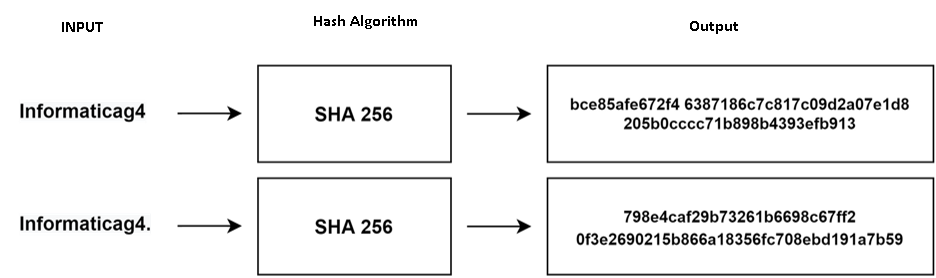
SHA256 este o funcție hash, nu o funcție de criptare. Din acest motiv, rezultatul datelor de ieșire SHA256 nu poate fi decriptat.
Mai multe informații despre SHA pot fi găsite aici: https://nvlpubs.nist.gov/nistpubs/FIPS/NIST.FIPS.180-4.pdf
SHA nu poate fi inversat deoarece este o funcție unidirecțională. Este ușor de calculat la fiecare intrare, dar dificil de calculat invers. Ar putea provoca un atac care nu și-ar atinge ținta de proiectare.
Exemplu SHA 256
Înainte de a începe procesul de hashing
Sunt declarate 8 valori hash inițiale
h0 = 0x6a09e667; h4 = 0x510e527f;
h1 = 0xbb67ae85; h5 = 0x9b05688c;
h2 = 0x3c6ef372; h6 = 0x1f83d9ab;
h3 = 0xa54ff53a; h7 = 0x5be0cd19
Acestea arată 32 de biți din rădăcina pătrată a primelor 8 numere prime
Pasul 1: Calculați rădăcina pătrată a numărului prim 2.
sqrt (2) - (1.4142135623730950488016887242097)
Pasul 2: Amintiți-vă partea sa zecimală.
(0.4142135623730950488016887242097)
Pasul 3: Înmulțiți cu 2 la puterea 32.
2 ^ 32 (0.4142135623730950488016887242097)
Rezultă: (1779033703.9520993849027770600526)
Pasul 4: valorile sunt reprezentate în format hexazecimal.
(6A09E667) = h0 = 0x6a09e667;
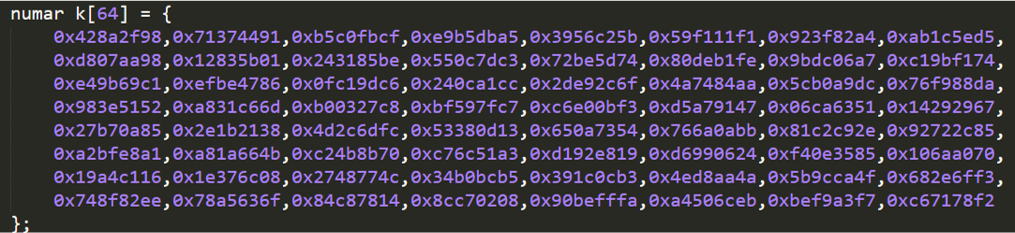
Acestea arată 32 de biți din radicalul primelor 64 de numere prime. Diferența față de calculul celor 8 valori hash inițiale este calculul părților fracționare ale rădăcinii cubice.
Exemplu de calcul:
Pasul 1: declarați 8 valori hash inițiale
Pasul 2: Declarați 64 de constante de hash
Pasul 3: De exemplu, datele de intrare „Informaticag4”
Codul ASCII pentru acestea este 7311010211111410997116105999710352
Pasul 4: Declarați o matrice w [0] - w [63] de tip data nesemnată lungă pe 32 de biți
Pasul 5: Mută 15 octeți ASCII în matricea de programare a mesajelor, începând cu w [0] și așa mai departe, apoi adăugați un bit '1' și '0' biți ca mai jos cu w [15] = lungimea datelor de intrare de biți (120 = 0x78)

Pasul 6: Calculați restul w [16] până la w [63]
Pasul 7: Declarați variabilele de lucru (a-h) și inițializați la valoarea hash curentă
Pasul 8: Creați funcția de compresie a buclei principale
Pasul 9: Adăugați hash-ul comprimat la valoarea hash curentă
Pasul 10: valoarea hash finală are loc h0 adăugare h1 adăugare h2 adăugare h3 adăugare h4 adăugare h5 adăugare h6 adăugare h7
Dacă pașii sunt executați corect, datele de intrare "Informaticag4" trebuie să aibă valoarea hash:
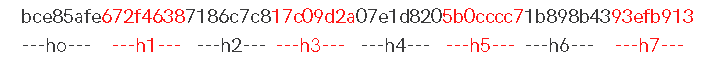
Rezultatul final