 Blocks
Blocks
Symmetric Key algorithms
At the base of the
symmetric key algorithm figures, of those that use for encryption a simple,
secret key, are the elementary figures the transposition and the substitution.[4]
The transposition
figures realize a permutation of the characters of the cleartext. The
encryption key is the pair K = (d, f), where d represents the length of the
successive blocks of characters that will be encrypted according to the
permutation f. The decryption is obtained by performing the inverse
permutation.
Substitution
cipher schemes replace each character in the message alphabet A with a
character in the C cryptogram alphabet.
If 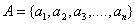 then
then 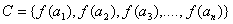 , where f substitution function, representing the key of the
algorithm. Its form is:
, where f substitution function, representing the key of the
algorithm. Its form is: 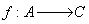 .
.
Traditional coding techniques are based
on the sender's and recipient's knowledge of the encryption key. The sender
encodes the message with a particular encoding system using the secret
encryption key, and the recipient decodes that information using the same
secret key. No other user needs to know the coding/decoding key.
There are two types of symmetrical
encoding: stream-level encryption and block-level encryption. Bit-level
encryption consists of encoding each bit of information, while at the block
level a certain number of message bits are encoded simultaneously (for example
64 bits), called a block. Symmetrical
encoding is faster than asymmetric encoding. A number of symmetric algorithms
can be implemented in hardware. In this way, an algorithm becomes faster in
operation.
There are two
types of symmetric encryption algorithms:
1.
Block
algorithms. Set
lengths of bits are encrypted in blocks of electronic data with the use of a
specific secret key. As the data is being encrypted, the system holds the data
in its memory as it waits for complete blocks.
2.
Stream
algorithms. Data is
encrypted as it streams instead of being retained in the system’s memory.
Some
examples of symmetric encryption algorithms include:
·
AES
(Advanced Encryption Standard)
·
DES (Data
Encryption Standard)
·
IDEA
(International Data Encryption Algorithm)
·
Blowfish
(Drop-in replacement for DES or IDEA)
·
RC4 (Rivest
Cipher 4)
·
RC5 (Rivest
Cipher 5)
·
RC6 (Rivest
Cipher 6)
AES, DES, IDEA,
Blowfish, RC5, and RC6 are block ciphers. RC4 is stream cipher.
The most commonly used symmetric algorithm is the Advanced
Encryption Standard (AES), which was originally known as Rijndael. This is the
standard set by the U.S. National Institute of Standards and Technology in 2001
for the encryption of electronic data announced in U.S. FIPS PUB 197[1]. This
standard supersedes DES, which had been in use since 1977. Under NIST, the AES
cipher has a block size of 128 bits, but can have three different key lengths
as shown with AES-128, AES-192 and AES-256.
Symmetrical
cryptography also has some disadvantages, such as:
-
Does not ensure the
authentication of the sender. This security gap does not allow the electronic
verification of certain transactions;
-
The transmission of the secret key between correspondents must be carried out on very secure channels.
-
When used between network
users, a large number of secret keys are required to communicate between two
users.
AES
One of the more popular and
widely adopted symmetric encryption algorithms likely to be encountered nowadays
is the Advanced Encryption Standard (AES). It is found at least six times faster
than triple DES.
A replacement for DES
was needed as its key size was too small. With increasing computing power, it
was considered vulnerable against exhaustive key search attacks. Triple DES was
designed to overcome this drawback but it was found slow.
The features of AES are:
·
Symmetric key symmetric block cipher
·
128-bit data, 128/192/256-bit keys
·
Stronger and faster than Triple-DES
·
Provide full specification and design details
·
Software implementable in C and Java
AES is an iterative
scheme. It is based on ‘substitution–permutation
network’. It comprises a series of linked operations, some of which
involve replacing inputs with specific outputs (substitutions) and others involve
shuffling bits around (permutations).
AES performs all
its computations on bytes rather than bits. Hence, AES treats the 128 bits of a
plaintext block as 16 bytes. These 16 bytes are arranged in four columns and
four rows for processing as a matrix −
The number of
rounds in AES are variable and depend on the length of the key. AES uses 10
rounds for 128-bit keys, 12 rounds for 192-bit keys, and 14 rounds for 256-bit
keys. Each of these rounds uses a different 128-bit round key, which is
calculated from the original AES key.
The schematic of
AES structure is illustrated in figure 2:
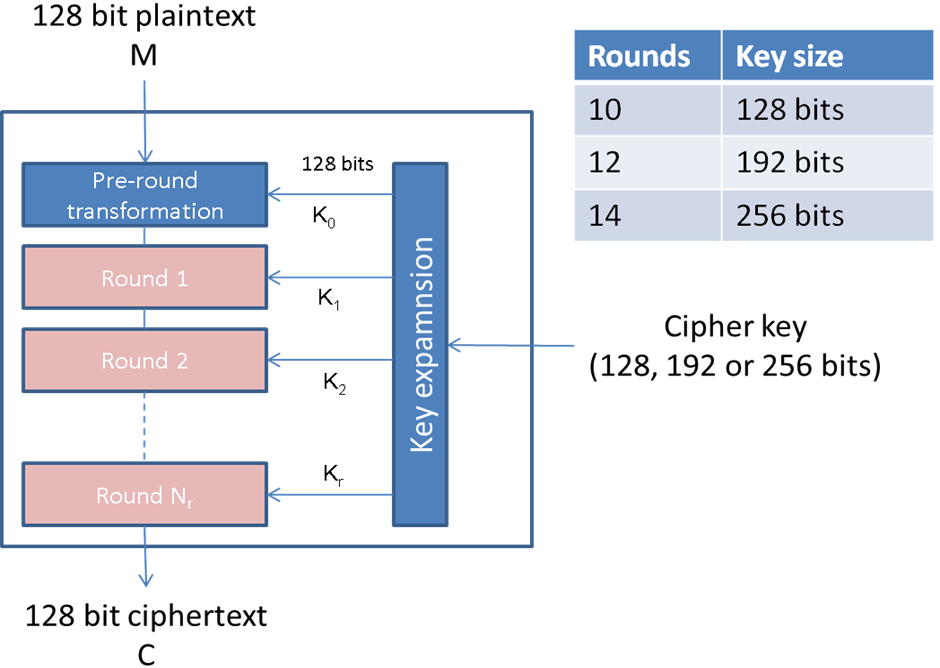
Figure
2. AES scheme
Encryption Process
Here, we restrict to
description of a typical round of AES encryption. Each round comprise four
sub-processes, as follows: AddRoundKey, SubBytes, ShiftRows, and MixColumns[1].
Pseudo Code for the AES cipher is:
Cipher(byte in[4*Nb], byte out[4*Nb], word w[Nb*(Nr+1)])
begin
byte state[4,Nb]
state = in AddRoundKey(state, w[0, Nb-1]) // See Sec. 5.1.4
for round = 1 step 1 to Nr–1
SubBytes(state)
ShiftRows(state)
MixColumns(state)
AddRoundKey(state, w[round*Nb, (round+1)*Nb-1])
end for
SubBytes(state)
ShiftRows(state)
AddRoundKey(state, w[Nr*Nb, (Nr+1)*Nb-1])
out = state
end
where:
Byte Substitution
(SubBytes)
The 16 input bytes are substituted by looking up a fixed table (S-box)
given in design. The result is in a matrix of four rows and four columns.
Shiftrows
Each of the four rows of the matrix is shifted to the left. Any entries
that ‘fall off’ are re-inserted on the right side of the row. The shift is carried out
as follows:
- The first row is not shifted.
- Second row is shifted one (byte)
position to the left.
- The third row is shifted two
positions to the left.
- The fourth row is shifted three
positions to the left.
- The result is a new matrix
consisting of the same 16 bytes but shifted with respect to each other.
- The first row is not shifted.
- Second row is shifted one (byte) position to the left.
- The third row is shifted two positions to the left.
- The fourth row is shifted three positions to the left.
- The result is a new matrix consisting of the same 16 bytes but shifted with respect to each other.
MixColumns
Each column of four bytes is now transformed using a special mathematical function. This function takes as input the four bytes of one column and outputs four completely new bytes, which replace the original column. The result is another new matrix consisting of 16 new bytes. It should be noted that this step is not performed in the last round.
Addroundkey
The 16 bytes of the matrix are now considered as 128 bits and are XORed to the 128 bits of the round key. If this is the last round then the output is the ciphertext. Otherwise, the resulting 128 bits are interpreted as 16 bytes and we begin another similar round.
Decryption Process
The process of the decryption of an AES ciphertext is similar to the encryption process in the reverse order. Each round consists of the four processes conducted in the reverse order :
- Add
round key
- Mix
columns
- Shift
rows
- Byte
substitution
Since sub-processes in each round are
in a reverse manner, the encryption and
decryption algorithms need to be separately implemented, although they are
very closely related, as follow:
InvCipher(byte in[4*Nb], byte out[4*Nb], word
w[Nb*(Nr+1)])
- Add round key
- Mix columns
- Shift rows
- Byte substitution
begin
byte state[4,Nb]
state = in
AddRoundKey(state, w[Nr*Nb, (Nr+1)*Nb-1])
for round = Nr-1 step -1 downto 1
InvShiftRows(state)
InvSubBytes(state)
AddRoundKey(state, w[round*Nb, (round+1)*Nb-1])
InvMixColumns(state)
end for
InvShiftRows(state)
InvSubBytes(state)
AddRoundKey(state, w[0, Nb-1])
out = state
end
In present-day
cryptography, AES is widely adopted and supported in both hardware and
software. Additionally, AES has built-in flexibility of key length, which
allows a degree of ‘future-proofing against progress in the ability to perform
exhaustive key searches. However, just as for DES, the AES security is assured
only if it is correctly implemented and good key management is employed.
AES has three
different key lengths. The main difference is the number of rounds that the
data goes through in the encryption process, 10, 12, and 14 respectively. In
essence, 192-bit and 256-bit provide a greater
security margin than 128-bit.
In the
current technological landscape, 128-bit AES is
enough for most practical purposes. Highly sensitive data handled by those with
an extreme threat level should probably be processed with either 192 or 256-bit
AES.
[1] https://nvlpubs.nist.gov/nistpubs/FIPS/NIST.FIPS.197.pdf
Ultima modificare: Friday, 21 May 2021, 10:11