Blocks
Blocks
Hash functions
A function that converts a given data to an integer value, we can assume a hash function is. The mapped integer value is used as an index in the hash table.
A hash function maps a big number or string to a small integer that can be used as the index in the hash table.
A good hash function should have the following properties:
- Efficiently computable.
- Should uniformly distribute the keys (Each table position equally likely for each key)
Simple hash functions
The following functions map a single integer key (k) to a small integer bucket value h(k). m is the size of the hash table (number of buckets).
Division method (Cormen) Choose a prime that isn't close to a power of 2. h(k) = k mod m. Works badly for many types of patterns in the input data.
Knuth Variant on Division h(k) = k(k+3) mod m. Supposedly works much better than the raw division method.
Multiplication Method (Cormen). Choose m to be a power of 2. Let A be some random-looking real number. Knuth suggests M = 0.5*(sqrt(5) - 1). Then do the following:
s = k*A
x = fractional part of s
h(k) = floor(m*x)
This seems to be the method that the theoreticians like.
To do this quickly with integer arithmetic, let w be the number of bits in a word (e.g. 32) and suppose m is 2^p. Then compute:
s = floor(A * 2^w)
x = k*s
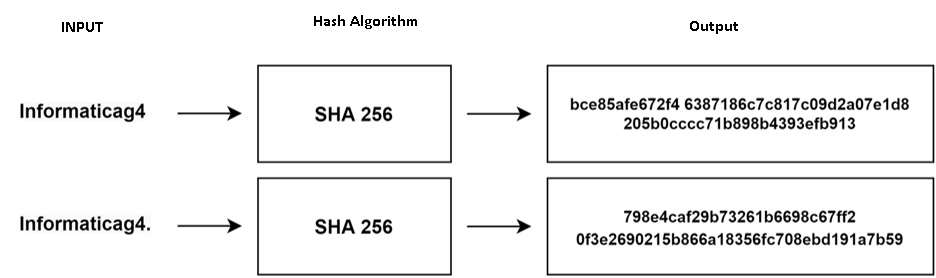
h(k) = x >> (w-p) SHA / Secure Hash AlgorithmThis Standard specifies secure hash algorithms, SHA-1, SHA-224, SHA-256, SHA-384, SHA512, SHA-512/224 and SHA-512/256. All of the algorithms are iterative, one-way hash functions that can process a message to produce a condensed representation called a message digest. These algorithms enable the determination of a message’s integrity: any change to the message will, with a very high probability, result in a different message digest. This property is useful in the generation and verification of digital signatures and message authentication codes, and in the generation of random numbers or bits.
SHA256 is a hash function, not an encryption function. For this reason, the result of the SHA256 output data cannot be decrypted.
More information about SHA can be found here: https://nvlpubs.nist.gov/nistpubs/FIPS/NIST.FIPS.180-4.pdf
SHA cannot be reversed because it is a one-way function. It is easy to calculate at each input, but difficult to calculate the reverse. It could cause an attack that would not reach its design target.
Example SHA 256
Before the hashing process begins
- 8 initial hash values are declared
h0 = 0x6a09e667; h4 = 0x510e527f;
h1 = 0xbb67ae85; h5 = 0x9b05688c;
h2 = 0x3c6ef372; h6 = 0x1f83d9ab;
h3 = 0xa54ff53a; h7 = 0x5be0cd19
Step 1: Calculate the square root of the prime number 2.
sqrt (2) - (1.4142135623730950488016887242097)
Step 2: Remember its decimal part.
(0.4142135623730950488016887242097)
Step 3: Multiply by 2 to power 32.
2 ^ 32 (0.4142135623730950488016887242097)
Result: (1779033703.9520993849027770600526)
Step 4: The values are presented in hexadecimal type.
(6A09E667) = h0 = 0x6a09e667;
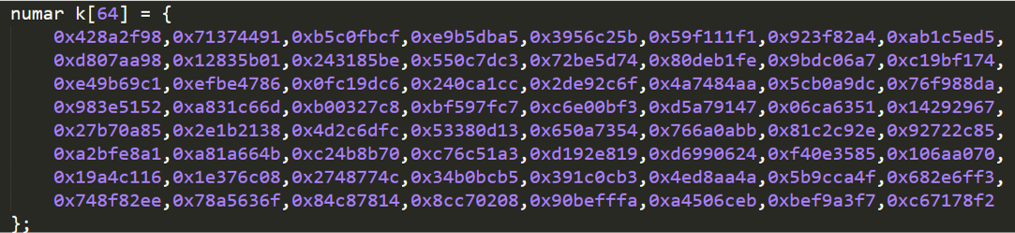
They show 32 bits of the radical of the first 64 prime numbers. The difference from the calculation of the 8 initial hash values is the calculation of fractional parts of the cubic root.
Calculus example:
Step 1: Declare 8 initial hash values
Step 2: Declare 64 hash constants
Step 3: For example, the input data "Informaticag4"
The ASCII code for these is 7311010211111410997116105999710352
Step 4: Declare an array w [0] - w [63] of type date unsigned long 32 bits
Step 5: Moves 15 ASCII bytes into the message programming array, starting with w [0] and so on, then add a bit '1' and '0' bits as below with w [15] = length of bit input data (120 = 0x78)

Step 6: Calculate the remainder w [16] to w [63]
Step 7: Declare the working variables (a-h) and initialize to the current hash value
Step 8: Create the main loop compression function
Step 9: Add the compressed hash to the current hash value
Step 10: The final hash value occurs h0 add h1 add h2 add h3 add h4 add h5 add h6 add h7
If the steps are executed correctly, the "Informaticag4" input data must have the hash value:
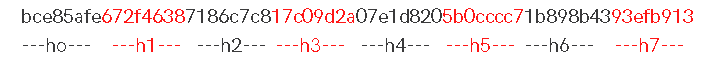
The complete result