 Blocks
Blocks
Asymmetric key algorithms
Asymmetric cryptographic algorithms have
emerged as an alternative to symmetric algorithms. Cryptography with public
(asymmetric) keys appeared in 1976 as a solution in secret key management. The
whole purpose of encryption is to keep a message secret. In the case of
symmetric cryptography, the process assumed that with the encoded message the
recipient should also hold or receive the decoding key.
Asymmetric cryptography is also known as
public-key cryptography. This means that different keys are used for encoding
and decoding processes. In this system, each correspondent holds a key pair: a
secret and a public key.
Public cryptography generally uses large
encryption keys to secure the strength of the algorithm. Comparing the length
of encryption keys between different algorithms is not always important and
productive at the same time. Even if public algorithms consume more time in the
coding operation than some symmetric methods, their use instead of symmetrical
ones are justified.
Cryptographic systems with public keys are of
asymmetric type. They have been developed especially in recent years, starting
from the reference works of Diffie and Hellman[3,5].
Rivest Shamir Adleman (RSA) Algorithm
The RSA encryption
is a public-key cryptosystem used for both encryption and authentication,
invented by Rivest, Shamir, and Adleman in 1977 [6,7].
The RSA system is
of exponential type. In this method the module n is obtained by the product of
two other large prime numbers: n = p * q, so that Euler's indicator
F(n)=(p-1)*(q-1). The latter becomes much more difficult to
determine, and the scheme can be successfully used in a public-key
cryptosystem.
In this method,
public keys e and n will be made public, and key d will be kept secret.
Regarding the method, it is recommended to choose a relatively d, prime number, with F
(n) in the range [max(p,q)+1, n-1].
In
this case, it will be calculated as follows:
e
= inv(d, F(n)), being able to use an extended
version of Euclid's algorithm.
Because
encryption and decryption are mutually inverse, the RSA method can be used for
both encryption and authentication. Each user owns the module and the exponents
e and d. Then he will record in a file the public key (consisting of n and e),
while he will keep the d key secret.
A
user B will issue a secret message M using the public transformation of A, as
follows:
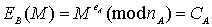
At the reception A
will get the message clearly, as follows:
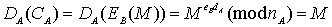
In the case of
authentication, the mechanism is the following:
User A will be
able to sign a message M to B by calculating:
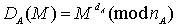
And B will
authenticate this message, using A's public key, as follows:
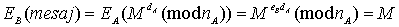
In this way, user B will know that that message comes from user A.
A difficulty in using RSA cryptosystems arises when both protection and
authentication are needed because successive transformations with different
modules are required.
For example, for A to send B a signed and encrypted message, A will
calculate:
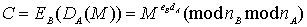
If
nA>nB the block
DA(M) Ï[0,nB-1]
corresponding EB.
Reducing
DA(M)mod nB does not solve the problem, not being able to
then get the original message. The
solution is to use a threshold h so that each user can construct two pairs of
transformations for signature and protection under the condition: nA1 < h < nA2
Last modified: Wednesday, 5 May 2021, 5:07 PM