Asymmetric cryptographic algorithms have emerged as an alternative to symmetric algorithms. Cryptography with public (asymmetric) keys appeared in 1976 as a solution in secret key management. The whole purpose of encryption is to keep a message secret. In the case of symmetric cryptography, the process assumed that with the encoded message the recipient should also hold or receive the decoding key.
Asymmetric cryptography is also known as public-key cryptography. This means that different keys are used for encoding and decoding processes. In this system, each correspondent holds a key pair: a secret and a public key.
Public cryptography generally uses large encryption keys to secure the strength of the algorithm. Comparing the length of encryption keys between different algorithms is not always important and productive at the same time. Even if public algorithms consume more time in the coding operation than some symmetric methods, their use instead of symmetrical ones are justified.
Cryptographic systems with public keys are of asymmetric type. They have been developed especially in recent years, starting from the reference works of Diffie and Hellman[3,5].
Rivest Shamir Adleman (RSA) Algorithm
The RSA encryption is a public-key cryptosystem used for both encryption and authentication, invented by Rivest, Shamir, and Adleman in 1977 [6,7].
The RSA system is of exponential type. In this method the module n is obtained by the product of two other large prime numbers: n = p * q, so that Euler's indicator
F(n)=(p-1)*(q-1).  The latter becomes much more difficult to determine, and the scheme can be successfully used in a public-key cryptosystem.
In this method, public keys e and n will be made public, and key d will be kept secret. Regarding the method, it is recommended to choose a relatively d, prime number,  with F (n) in the range [max(p,q)+1, n-1].
In this case, it will be calculated as follows:
e = inv(d, F(n)), being able to use an extended version of Euclid's algorithm.
Because encryption and decryption are mutually inverse, the RSA method can be used for both encryption and authentication. Each user owns the module and the exponents e and d. Then he will record in a file the public key (consisting of n and e), while he will keep the d key secret.
A user B will issue a secret message M using the public transformation of A, as follows:

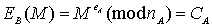
 At the reception A will get the message clearly, as follows:

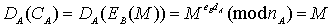
In the case of authentication, the mechanism is the following:
User A will be able to sign a message M to B by calculating:

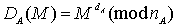
And B will authenticate this message, using A's public key, as follows:

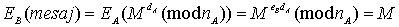
 In this way, user B will know that that message comes from user A.
A difficulty in using RSA cryptosystems arises when both protection and authentication are needed because successive transformations with different modules are required.
For example, for A to send B a signed and encrypted message, A will calculate:

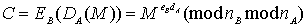
If n_A>n_B the block  D_A(M) Ï[0,n_B-1] corresponding E_B.
Reducing D_A(M)mod n_B does not solve the problem, not being able to then get the original message.  The solution is to use a threshold h so that each user can construct two pairs of transformations for signature and protection under the condition:  n_{A1 < h <} n_A2